PWC 200

This week again, due to work pressures, I have done the challenges only in Perl 5 and Raku, not in the guest language Julia.

Challenge 1 (Arithmetic Slices)

Given a list of integers, we are asked to find all slices of the list (sub-lists of consecutive elements) that have at least three elements, and where the difference between every consecutive element is the same.

This is a one-liner in Raku.

raku -e '(0 .. @*ARGS-1).combinations(2).grep({@_[1]-@_[0]>1}).map({@*ARGS[@_[0]..@_[1]]}).grep( {my @n=@_; (0 .. @n-3).map( {(@n[$_+1]-@n[$_]) == (@n[$_+2]-@n[$_+1])} ).sum==(@n.elems-2) } ).say' $@

The steps are:

1. Get all slices by getting all combinations of two elements (bounds of the slice)
2. Restrict to slices that are at least three elements long (difference between the slice bounds is greater than 1)
3. Map the pairs of bounds to get slices from the list
4. Use grep to check if the condition is true for each slice:
1. For each slice, loop through the slice, checking that the distance between every two consecutive elements n,n+1 is the same as that between the adjacent (overlapping) pair of consecutive elements n+1, n+2
2. Since this gives a list of boolean values, sum them up to verify that it is True for every step in the iteration (true if the sum is equal to the number of iterations in the previous step)

This looks inefficient in theory, but I would assume that the compiler and VM take care of some optimizations behind the scenes.

My Perl 5 script is a direct translation, but I did not make it a one-liner. That would be cumbersome as I use three modules: Data::Dumper, List::Util, and Algorithm::Combinatorics to give me the equivalent of 'say', 'sum' and 'combinations' from Raku.

 Perl 5 subroutine:

sub arithmetic_slices {
    my (@arry) = @_;

    (scalar(@_) <= 2) && (return []);

    return (
    grep {my @n=$_->@*;    
        sum (map {($n[$_+1] - $n[$_]) == ($n[$_+2] - $n[$_+1]) }
        (0 .. @n-3) ) == @n-2;
        }
    map {[@arry[$_->[0] .. $_->[1]]]}
    grep {$_->[1] - $_->[0] > 1}
    combinations [0 .. @arry-1], 2 );
}

Challenge 2 (Seven Segment 200)

We are asked to generate an ASCII-art simulation of a digital display of numbers, with 200 as the test example. The spec gives a particular truth table based on a mapping of the letters 'a' through 'g' with the edges of the digital number in a 7 characters x 7 lines display as in:

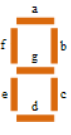
I find it easier to use the following four strings, which I store as constants using the names hl, v_, _v, v_v respectively.

hl:     '-------'

v_:    '|      '

_v:    '     |'

v_v:  '|     |'

 

Then for example, the number 8 can be represented as the array: 

 

[hl,v_v,v_v,hl,v_v,v_v,hl]

 

Print out the elements separated by "\n" and you have the ASCII representation of 8.

 

To print out a multi-digit number, say 200, you just iterate through the arrays corresponding to the digits, say if the array for digit is stored in an array of arrays as encoded[digit]:

 

Print encoded[2]->[0]," ", encoded[0]->[0]," ", encoded[0]->[0],"\n";

Print encoded[2]->[1]," ",encoded[0]->[1]," ", encoded[0]->[1],"\n"; ...

 

Raku is a direct translation of the Perl 5 version. 

 

My encoding can be mapped to the 'abcdefg' truth table, though it's a bit tedious. For example, f and b true corresponds to elements 1 and 2 in my array being v_v. 

Perl 5 script here

Raku script here